Carrasco, M., Bernardez, G., Montagna, M., Miolane, N., Telyatnikov, L.
Abstract
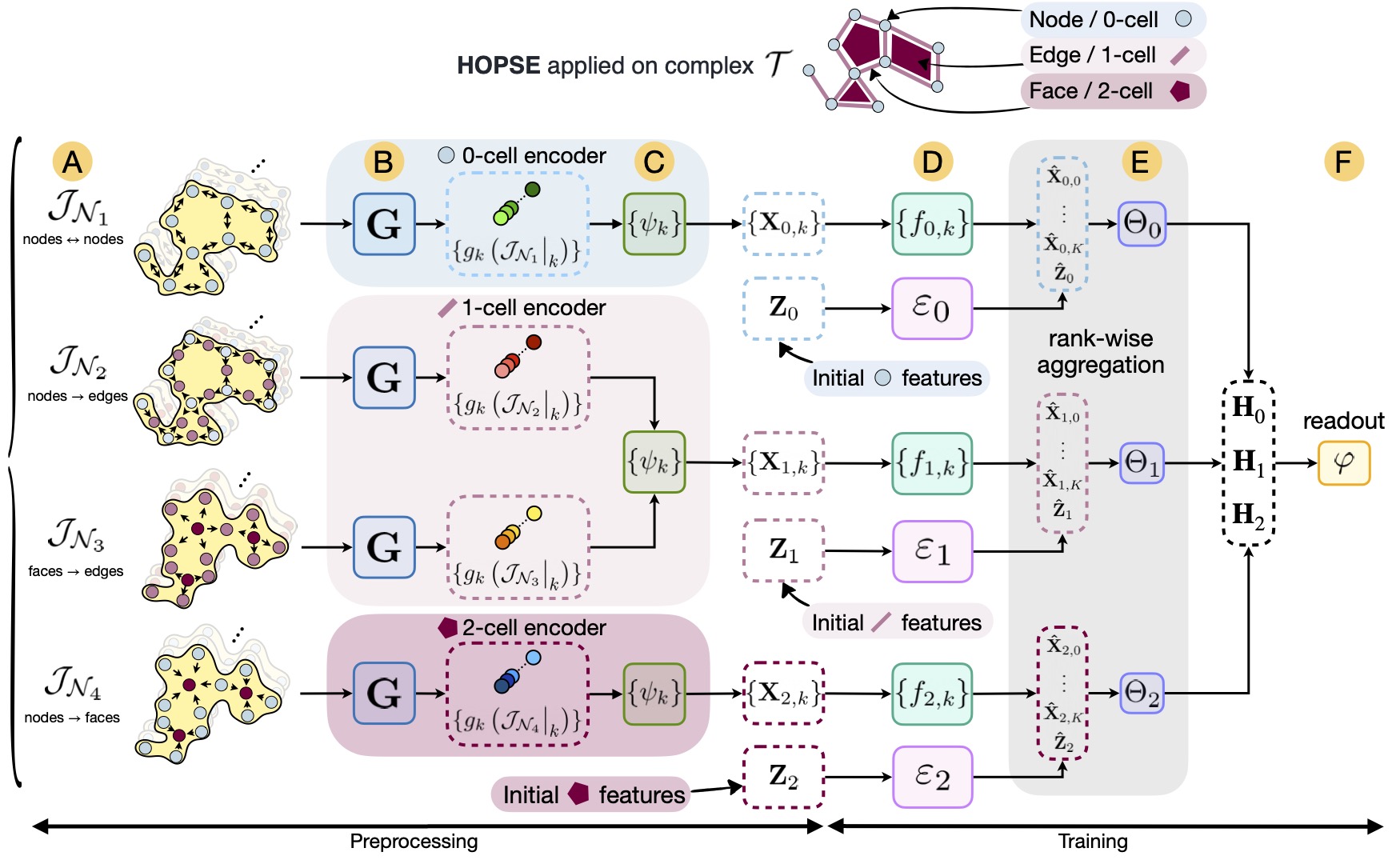
While Graph Neural Networks (GNNs) have proven highly effective at modeling relational data, pairwise connections cannot fully capture multi-way relationships naturally present in complex real-world systems. In response to this, Topological Deep Learning (TDL) leverages more general combinatorial representations -- such as simplicial or cellular complexes -- to accommodate higher-order interactions. Existing TDL methods often extend GNNs through Higher-Order Message Passing (HOMP), but face critical \emph{scalability challenges} due to \textit{(i)} a combinatorial explosion of message-passing routes, and \textit{(ii)} significant complexity overhead from the propagation mechanism. To overcome these limitations, we propose HOPSE (Higher-Order Positional and Structural Encoder) -- a \emph{message passing-free} framework that uses Hasse graph decompositions to derive efficient and expressive encodings over \emph{arbitrary higher-order domains}. Notably, HOPSE scales linearly with dataset size while preserving expressive power and permutation equivariance. Experiments on molecular, expressivity and topological benchmarks show that HOPSE matches or surpasses state-of-the-art performance while achieving up to 7 times speedups over HOMP-based models, opening a new path for scalable TDL.
Citation
Carrasco, M., Bernardez, G., Montagna, M., Miolane, N., & Telyatnikov, L. (2025). HOPSE: Scalable Higher-Order Positional and Structural Encoder for Combinatorial Representations. arXiv preprint arXiv:2505.15405.
BibTeX
@article{carrasco2025hopse,
title={HOPSE: Scalable Higher-Order Positional and Structural Encoder for Combinatorial Representations},
author={Carrasco, Martin and Bernardez, Guillermo and Montagna, Marco and Miolane, Nina and Telyatnikov, Lev},
journal={arXiv preprint arXiv:2505.15405},
year={2025}
}