Unsupervised Cell Segmentation by Fast Gaussian Processes | The New England Journal of Statistics in Data Science
Baracaldo, L., King, B., Yan, H., Lin, Y., Miolane, N., Gu, N.
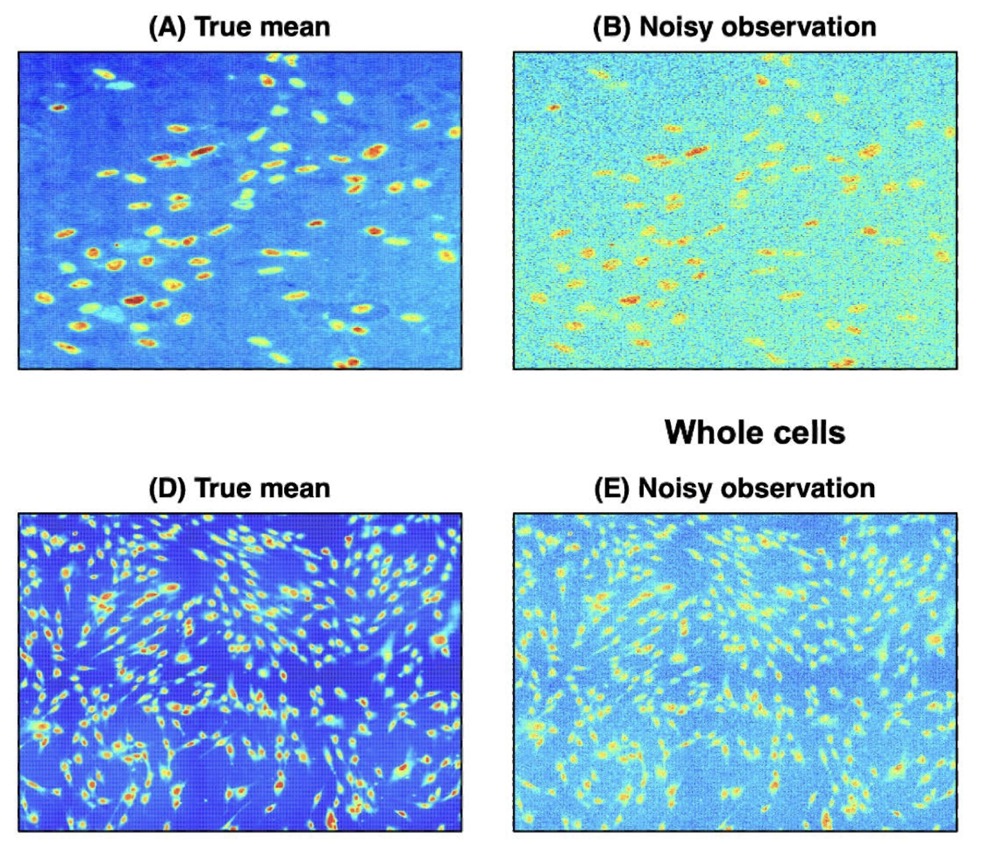
We present an unsupervised cell segmentation method based on fast Gaussian processes that accurately handles noisy, heterogeneous microscopy images without parameter tuning, shape assumptions, or labeled data, and outperforms existing approaches in both simulated and large-scale real datasets.
GraphUniverse: Enabling Systematic Evaluation of Inductive Generalization | ICLR
Van Langendonck, L., Bernárdez, G., Miolane, N., Barlet-Ros, P.
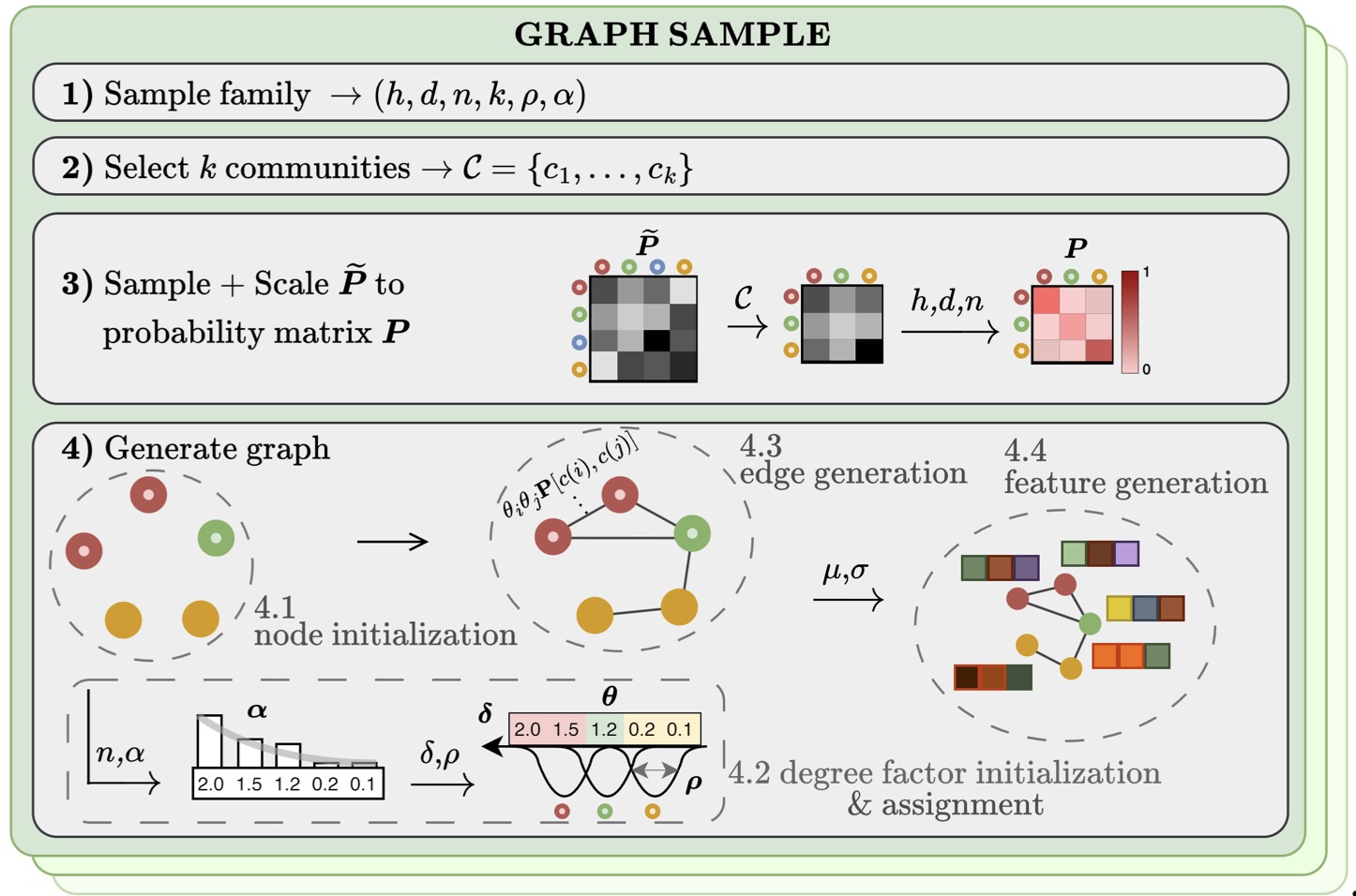
We introduce GraphUniverse, a scalable framework that generates families of graphs with persistent semantic communities to systematically evaluate inductive generalization and robustness to distribution shifts, revealing that strong transductive performance poorly predicts generalization across diverse graph architectures and regimes.
Understanding Benefit of Personalization: Beyond Classification | ICLR
Cornelis, L., Bernardez, G., Jeong, H., & Miolane, N.
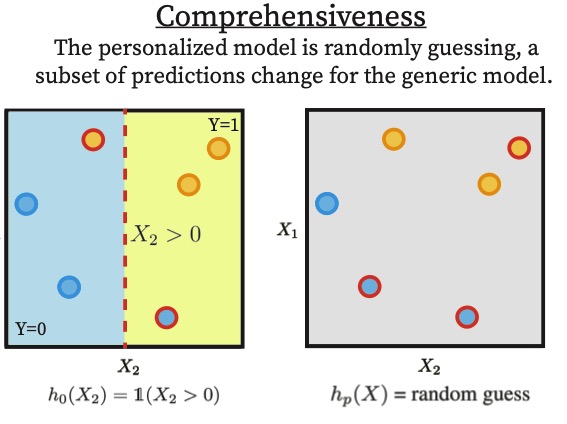
This work introduces a unified framework to evaluate personalization in machine learning by jointly quantifying its impact on predictive performance and explanation quality across groups, demonstrating theoretically and empirically that gains in accuracy do not necessarily imply improved explainability, even in safety-critical settings.

Bounds on the geodesic distances on the Stiefel manifold for a family of Riemannian metrics | Linear Algebra and its Applications
Mataigne, S., Absil, P.A., Miolane, N.
The work enhances geodesic computation on the Stiefel manifold by analyzing a family of Riemannian metrics with distances equivalent to the Frobenius norm and introducing SkewLinearAlgebra.jl, a Julia package for efficient skew-symmetric matrix operations.
Read More
Latent Computing by Biological Neural Networks: A Dynamical Systems Framework | Preprint
Dinc, F., Blanco-Pozo, M., Klindt, D., Acosta, F., Jiang, Y., Ebrahimi, S., Shai, A., Tanaka, H., Yuan, P., Schnitzer, M. J., & Miolane, N.
We propose a dynamical systems framework centered on latent processing units to explain how neural circuits perform robust computations despite representational drift, identifying five key attributes that link low-dimensional computation, coding redundancy, linear decodability, and stability across time and scale.
Read More
Understanding and Controlling the Geometry of Memory Organization in RNNs | Preprint
Haputhanthri, U., Storan, L., Jiang, Y., Raheja, T., Shai, A., Akengin, O., Miolane, N., Schnitzer, M. J., Dinc, F., & Tanaka, H
We investigate abrupt learning in RNNs trained on short-term memory tasks, showing that geometric restructuring in phase space precedes sudden performance gains, and introduce a temporal consistency regularization that promotes efficient, biologically plausible learning and attractor formation.
Read More
Beyond Manifolds: Learning on Graphs and Trees with Geodesic Metric Spaces | Preprint
Calissano, A., Pereira, L., Lueg, J., Miolane, N.
We present a Python package—built as a Geomstats plug-in—for analyzing datasets of graphs and trees as strongly non-Euclidean data in geodesic metric spaces, leveraging their connections to Euclidean and Riemannian structures, with a modular design, practical examples, and full documentation.
Read More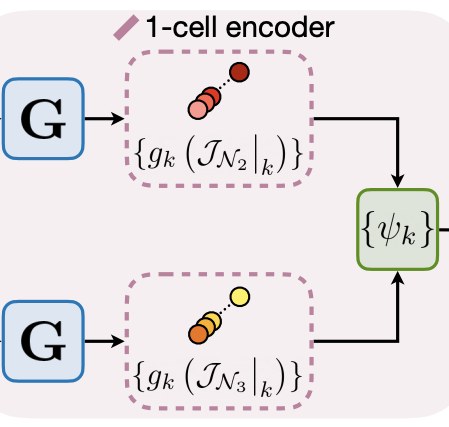
HOPSE: Scalable Higher-Order Positional and Structural Encoder for Combinatorial Representations | Preprint
Carrasco, M., Bernardez, G., Montagna, M., Miolane, N., Telyatnikov, L.
Graph Neural Networks (GNNs) model pairwise relations well but struggle with the higher-order interactions present in many real-world systems. Topological Deep Learning (TDL) extends GNNs using higher-order message passing (HOMP) on simplicial or cellular complexes, but suffers from combinatorial blowup and high complexity. To address this, HOPSE (Higher-Order Positional and Structural Encoder) avoids message passing entirely, instead using Hasse graph decompositions for efficient, expressive encodings. HOPSE scales linearly with data size, maintains expressive power and permutation equivariance, and achieves state-of-the-art accuracy with up to 7× speedups over HOMP-based models across molecular, expressivity, and topological benchmarks—opening a scalable path for TDL.
Read More
Alternating Gradient Flows: A Theory of Feature Learning in Two-layer Neural Networks | NeurIPS
Kunin, D., Luca Marchetti, G., Chen, F., Karkada, D., B. Simon, J., R. DeWeese, M., Ganguli, S., Miolane, N.
This paper introduces Alternating Gradient Flows (AGF), a framework that models feature learning in two-layer networks trained from small initialization as an alternating process of neuron activation and loss minimization. AGF explains the timing and structure of loss drops during training, unifying prior analyses and revealing that networks learn features like principal components or Fourier modes in a predictable order.
Read More
Ordered Topological Deep Learning: A Network Modeling Case Study | Preprint
Bernárdez. G. , Ferriol-Galmés, M., Güemes-Palau, C., Papillon, M., Barlet-Ros, P., Cabellos-Aparicio, A., Miolane, N.
Computer networks underpin modern digital infrastructure, but traditional modeling methods often fall short due to high computational cost or restrictive assumptions. Deep learning–based models such as RouteNet have redefined network modeling, offering a powerful balance between accuracy and efficiency. In this work, we reveal RouteNet’s hidden foundation in Topological Deep Learning and introduce OrdGCCN, a novel ordered topological framework that demonstrates the first successful real-world application of TDL principles.
Read More
GeomFuM: A Python Package for Machine Learning with Functional Maps |
Viganò, G., Longari, G., F. Pereira, L., Miolane, N., Melzi, S.
We present GeomFuM, an open-source Python library for geometry processing and machine learning on functional maps, offering modular, tested implementations for spectral geometry, functional map algorithms, and shape analysis tasks. Supporting NumPy and PyTorch backends, it enables efficient research and development in 3D geometry, geometric deep learning, and related fields.
Dynamical Phases of Short-Term Memory Mechanisms in RNNs | ICML
Kurtkaya, B., Dinc, F., Yuksekgonul, M., Blanco-Pozo, M., Cirakman, E., Schnitzer, M., Yemez, Y., Tanaka, H., Yuan, P., & Miolane, N.
We uncover two distinct mechanisms—slow-point manifolds and limit cycles—that support short-term memory in recurrent networks, derive theoretical scaling laws governing their emergence, and validate these findings across 35,000 RNNs, offering new insights and testable predictions for neuroscience.
Read More
TopoTune : A Framework for Generalized Combinatorial Complex Neural Networks | ICML
Papillon, M., Bernárdez, G., Battiloro, C., Miolane, N.
We introduce Generalized Combinatorial Complex Neural Networks (GCCNs), a simple yet powerful family of Topological Deep Learning (TDL) models that generalize CCNNs, systematically extend graph neural networks to higher-order domains, and, through the TopoTune framework, enable flexible and accessible development of expressive TDL architectures.
Read More
TopoBench: A Framework for Benchmarking Topological Deep Learning | DMLR
Telyatnikov, L., Bernardez, G., Montagna, M., Vasylenko, P., Zamzmi, G., Hajij, M., Schaub, M., Miolane, N., Scardapane, S., Papamarkou, T.
TopoBenchmarkX is a modular open-source library that standardizes and accelerates research in Topological Deep Learning by enabling flexible benchmarking, transformation across topological domains, and evaluation of diverse TDL architectures.
Read More
Beyond Euclid: An Illustrated Guide to Modern Machine Learning with Geometric, Topological, and Algebraic Structures | MLST
Papillon, M., Sanborn, A., Mathe, J., Cornelis, L., Bertics, A., Buracas, D., Lillemark, H., Shewmake, C., Dinc, F., Pennec, X., Miolane, N.
The emerging field of non-Euclidean machine learning generalizes classical methods to data with complex geometric, topological, and algebraic structures, offering a unified graphical taxonomy of recent advances along with insights into key challenges and future opportunities.
Read More
Flow Tree: A Dynamical Classifier for Quantifying Navigation Paths and Strategies | CoSyNe
Bertics, A., Chrastil, E., Miolane, N., & Carlson, J.
We introduce the Flow Tree, a novel data structure adapted from the Reeb graph, to capture and analyze dynamic navigation behaviors across multiple trajectories, enabling improved prediction of path difficulty and individual navigation success. Applied to VR maze data from 100 participants, Flow Trees outperform static metrics and reveal distinct strategies used by good versus poor navigators.
Read More
On the Approximation of the Riemannian Barycenter | GSI (oral)
Mataigne, S., Absil, P.-A., Miolane, N.
We present a method to compute an approximate Riemannian barycenter of a collection of points lying on a Riemannian manifold. Our approach relies on the use of theoretically proven under- and overapproximations of the Riemannian distance function. We compare it to the exact computation of the Riemannian barycenter and to an approach that approximates the Riemannian logarithm using lifting maps. Experiments are conducted on the Stiefel manifold.
Read More
Learning Riemannian Metrics for Interpolating Animations | GSI (oral)
Kushner, S., Modi, V., Miolane, N.
We present a method for upsampling low frame rate animations by interpolating character bone orientations along geodesics from a family of invariant Riemannian metrics on SO(3) products. An optimization step selects the best-fitting metric for compression, yielding results that outperform existing techniques.
Read More
Learning from Landmarks, Curves, Surfaces, and Shapes in Geomstats | TOMS
Pereira, L., Le Brigant, A., Myers, A., Hartman, E., Khan, A., Tuerkoen, M., Dold, T., Gu, M., Suárez-Serrato, P., Miolane, N.
We introduce the shape module of the Geomstats Python package, which provides tools for analyzing shape data—landmarks, curves, and surfaces—via implemented shape spaces, Riemannian geometry, and abstract mathematical structures, enabling statistical and machine learning tasks through a modular, object-oriented design with illustrative examples.
Read More
Global Distortions from Local Rewards: Neural Coding Strategies in Path-Integrating Neural Systems | NeurIPS
Acosta, F., Dinc, F., Redman, W., Madhav, M., Klindt, D., Miolane, N.
Grid cells, traditionally understood to encode physical location, exhibit globally distorted firing patterns in response to rewarded landmarks; by training path-integrating recurrent neural networks, this study reveals how spatial and reward information integrate in grid-like codes, offering a framework that bridges computational modeling with biologically grounded spatial navigation.
Read More
Not So griddy: Internal Representations of RNNs Path Integrating More Than One Agent | NeurIPS
Redman W., Acosta, F., Acosta-Mendoza, S., Miolane, N.
We show that RNNs trained to path integrate multiple agents develop distinct unit- and population-level representations - such as weaker grid cells, stronger border cells, and relative position tuning - highlighting how multi-agent navigation shapes spatial coding and neural dynamics.
Read More
The Selective G-Bispectrum and its Inversion: Applications to G-Invariant Networks | NeurIPS
Mataigne, S., Mathe, J., Sanborn, S., Hillar, C., Miolane, N.
We present the selective G-Bispectrum, a computationally efficient alternative to the full G-Bispectrum with O(|G|) complexity, which retains key invariance properties for group actions and enhances neural network performance in terms of accuracy, robustness, and speed.
Read More
ICML 2024 Topological Deep Learning Challenge: Design and Results | PMLR
Bernárdez, G., Telyatnikov, L., Montagna, M., Baccini, F., Papillon, M., Miolane, N., et al.
The 2nd ICML Topological Deep Learning Challenge, held at the ICML 2024 GRaM Workshop, focused on designing topological liftings between discrete data structures and topological domains, receiving 52 qualifying submissions and yielding key insights into bridging TDL with structured datasets.
Read More
Position: Topological Deep Learning is the New Frontier for Relational Learning | ICML
Papamarkou, T., Birdal, T., Bronstein, M., Carlsson, G., Curry, J., Gao, Y., Hajij, M., Kwitt, R., Liò, P., Di Lorenzo, P., Maroulas, V., Miolane, N., Nasrin, F., Natesan Ramamurthy, K., Rieck, B., Scardapane, S., T. Schaub, M., Veličković, P., Wang, B., Wang, Y., Wei, G., Zamzmi, G.
This paper explores topological deep learning as a complementary approach to graph and geometric learning, outlining key open problems, potential solutions, and future research directions in the field.
Read More
On Accuracy and Speed of Geodesic Regression: Do Geometric Priors Improve Learning on Small Datasets? | CVPR-W
Myers, A., Miolane, N.
A theoretical and empirical study questions whether the accuracy gains of geodesic regression on manifolds justify the significant computational cost compared to linear methods.
Read More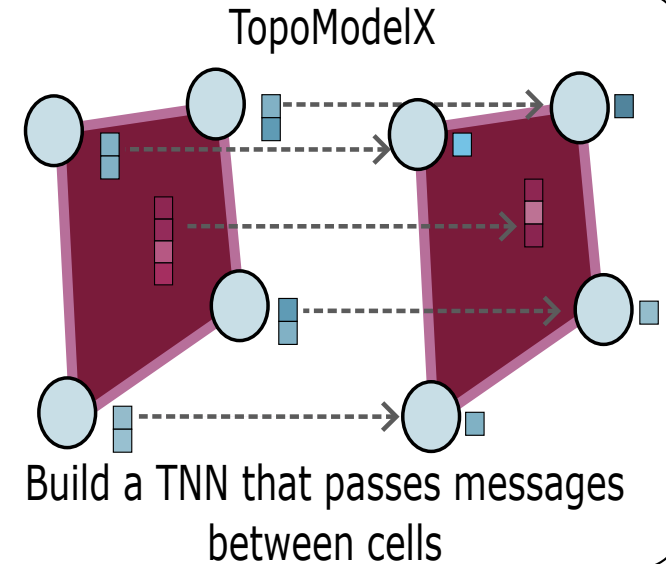
TopoX: A Suite of Python Packages for Machine Learning on Topological Domains | JMLR
Hajij, M., Papillon, M., Frantzen, F., Agerberg, J., AlJabea, I., Ballester, R., Battiloro, C., Bernárdez, G., Birdal, T., Brent, A., Chin, P., Escalera, S., Fiorellino, S., Hoff Gardaa, O., Gopalakrishnan, G., Govil, D., Hoppe, J., Reddy Karri, M., Khouja, J., Lecha, M., Livesay, N., Meißner, J., Mukherjee, S., Nikitin, A., Papamarkou, T., Prílepok, J., Natesan Ramamurthy, K., Rosen, P., Guzmán-Sáenz, A., Salatiello, A., N. Samaga, S., Scardapane, S., T. Schaub, M., Scofano, L., Spinelli, I., Telyatnikov, L., Truong, Q., Walters, R., Yang, M., Zaghen, O., Zamzmi, G., Zia, A., Miolane, N.
TopoX is a Python suite for computing and machine learning on advanced topological domains, featuring tools for construction (TopoNetX), embedding (TopoEmbedX), and neural modeling (TopoModelX), with open-source code under the MIT license.
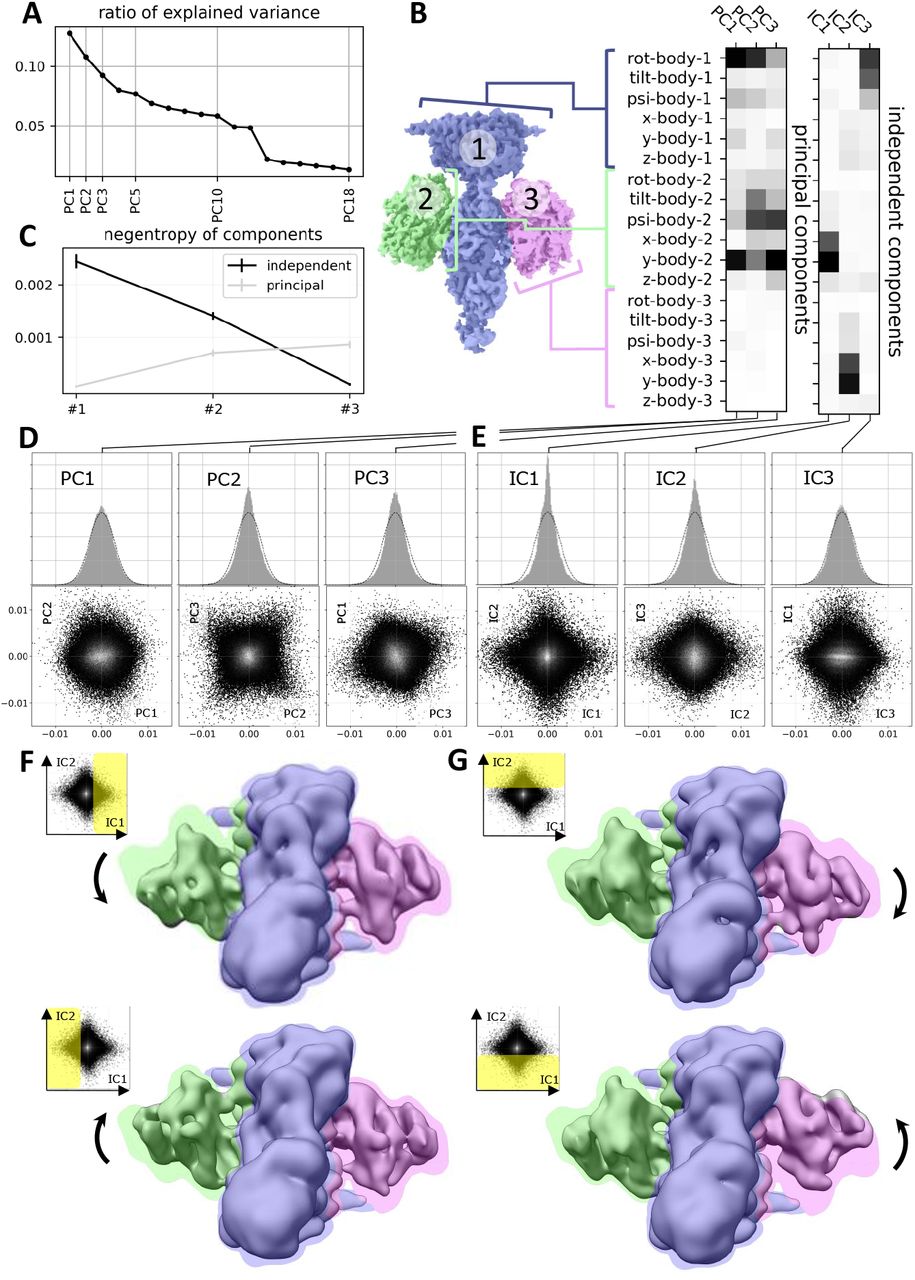
Towards Interpretable Cryo-EM: Disentangling Latent Spaces of Molecular Conformations | Frontiers in Molecular Biosciences
A. Klindt, D., Hyvärinen, A., Levy, A., Miolane, N., Poitevin, F.
Interpreting cryo-EM latent spaces as a nonlinear ICA problem enables the discovery of identifiable, disentangled molecular conformations with broad implications for structural biology and AI-driven scientific discovery.
Read More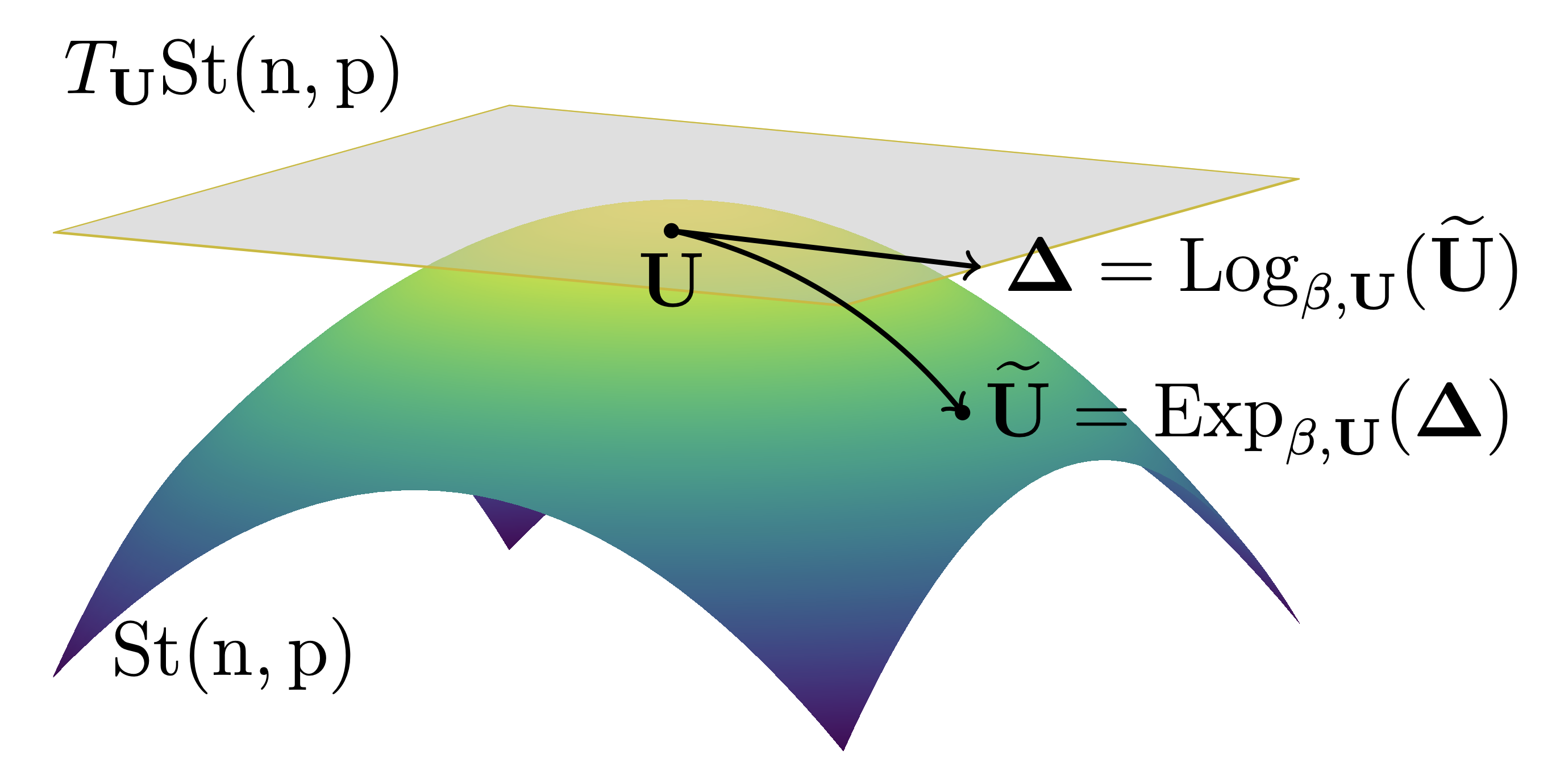
An Efficient Algorithm for the Riemannian Logarithm on the Stiefel Manifold for a Family of Riemannian Metrics | SIAM Journal on Matrix Analysis and Applications (SIMAX)
Mataigne, S., Zimmermann, R., Miolane, N.
An efficient matrix-algebraic method is introduced to compute the Riemannian Log across a one-parameter family of metrics on the Stiefel manifold, unifying and extending prior approaches.
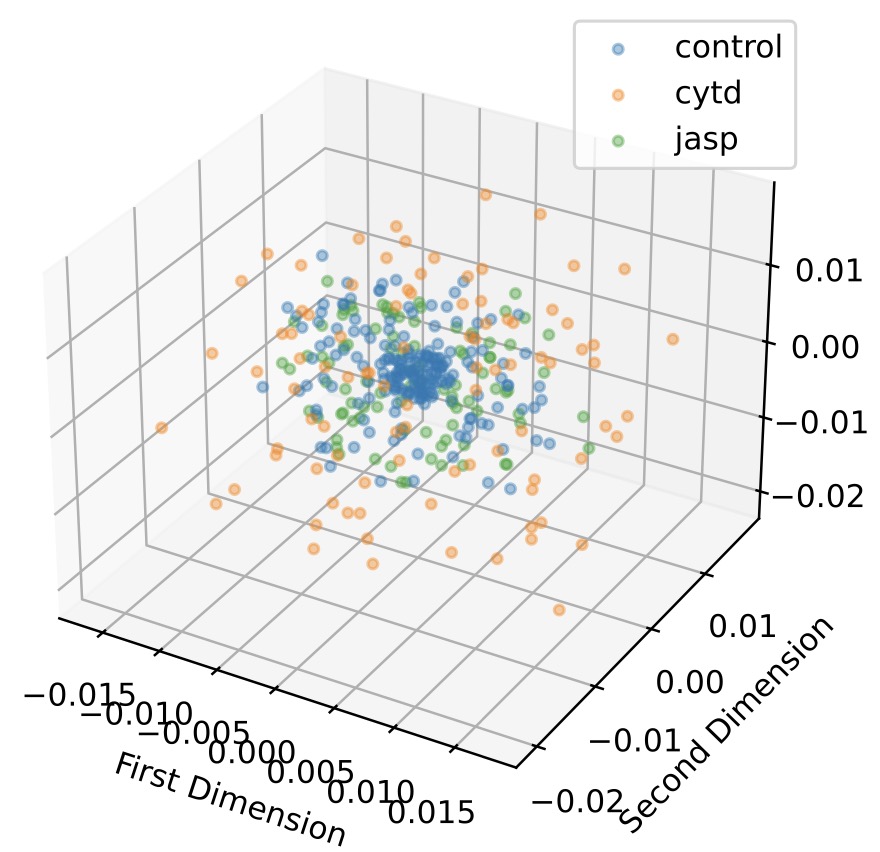
Unveiling Cellular Morphology: Statistical Analysis Using a Riemannian Elastic Metric in Cancer Cell Image Datasets | Information Geometry
Li, W., Prasad, A., Miolane, N., Dao Duc, K.
The Square Root Velocity (SRV) metric offers improved characterization of cell shape heterogeneity and enhances classification of cancer-treated cells, outperforming linear metrics in both interpretability and accuracy.
Read More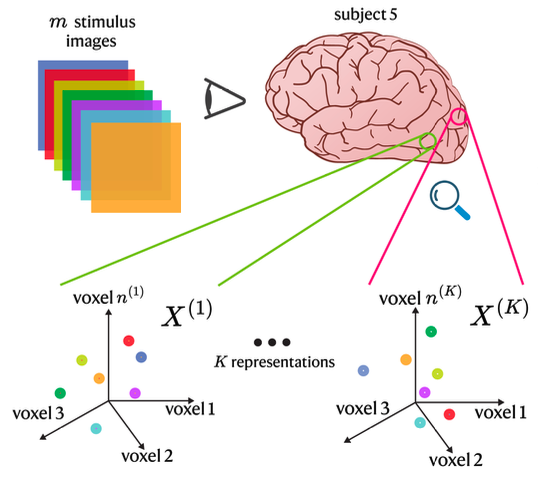
Relating Representational Geometry to Cortical Geometry in the Visual Cortex | NeurIPS Workshop on Unifying Representations in Neural Models
Acosta, F., Conwell, C., Sanborn, S., Klindt, D., Miolane, N.
We evaluate representational similarity methods by how well they reflect cortical anatomy, finding that first-order metrics best capture consistent brain–representation alignment across individuals.
Read More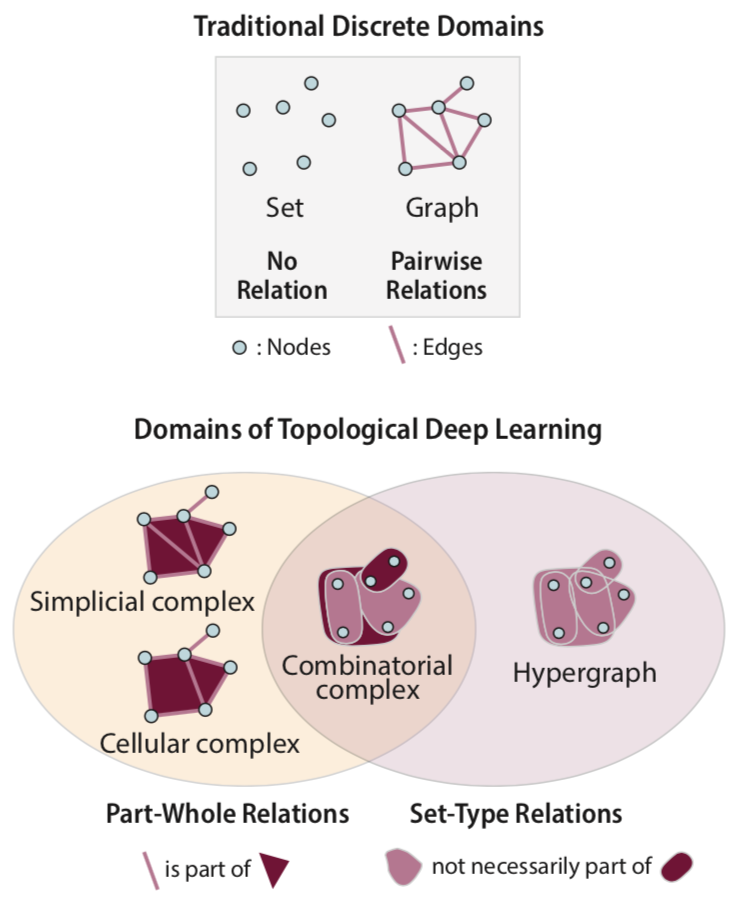
ICML 2023 Topological Deep Learning Challenge: Design and Results | PMLR
Papillon, M., Hajij, M., Myers, A., Jenne, H., Mathe, J., Papamarkou, T., ... & Miolane, N.
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two month duration. This paper describes the design of the challenge and summarizes its main findings.
Read More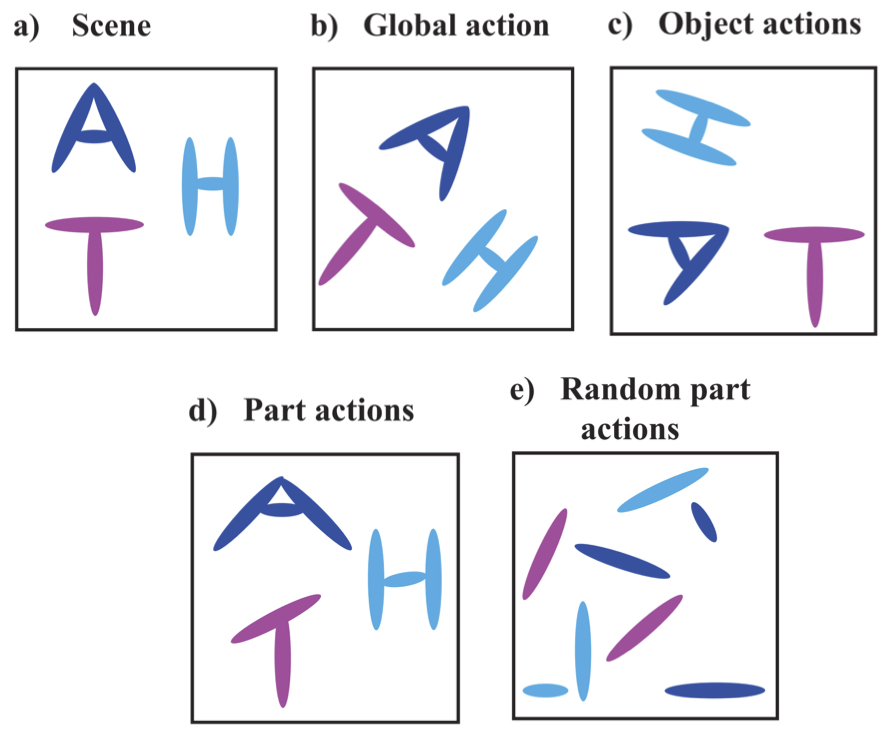
Visual Scene Representation with Hierarchical Equivariant Sparse Coding | PMLR
Shewmake, C., Buracas, D., Lillemark, H., Shin, J., Bekkers, E., Miolane, N., Olshausen, B.
A hierarchical neural network is proposed for unsupervised learning of part-whole scene decompositions, achieving hierarchical equivariance via Bayesian inference to mimic visual cortex-like perceptual processing.
Read More
Preface: NeurIPS Workshop on Symmetry and Geometry in Neural Representations | PMLR
Sanborn, S., Shewmake, C., Azeglio, S., Di Bernardo, A., Miolane, N.
The first annual NeurIPS Workshop on Symmetry and Geometry in Neural Representations (NeurReps) was conceived to bring together researchers at the nexus of applied geometry, deep learning, and neuroscience, with the goal of advancing this understanding and illuminating geometric principles for neural information processing. Ultimately, we hope that this venue and associated community will support the development of the geometric approach to understanding neural representations, while strengthening ties to the mathematics community. The Neural Information Processing Systems (NeurIPS) conference historically emerged from the field of theoretical neuroscience or “connectionism.” This venue thus further serves the workshop’s goal of reinforcing the bond between deep learning and neuroscience.
Read More
A General Framework for Robust G-Invariance in G-Equivariant Networks | NeurIPS
Sanborn, S., Miolane, N.
We introduce a general method for achieving robust group-invariance in group-equivariant convolutional neural networks (G-CNNs), which we call the G-triple-correlation (G-TC) layer. The approach leverages the theory of the triple-correlation on groups, which is the unique, lowest-degree polynomial invariant map that is also complete. Many commonly used invariant maps - such as the max - are incomplete: they remove both group and signal structure. A complete invariant, by contrast, removes only the variation due to the actions of the group, while preserving all information about the structure of the signal.
Read More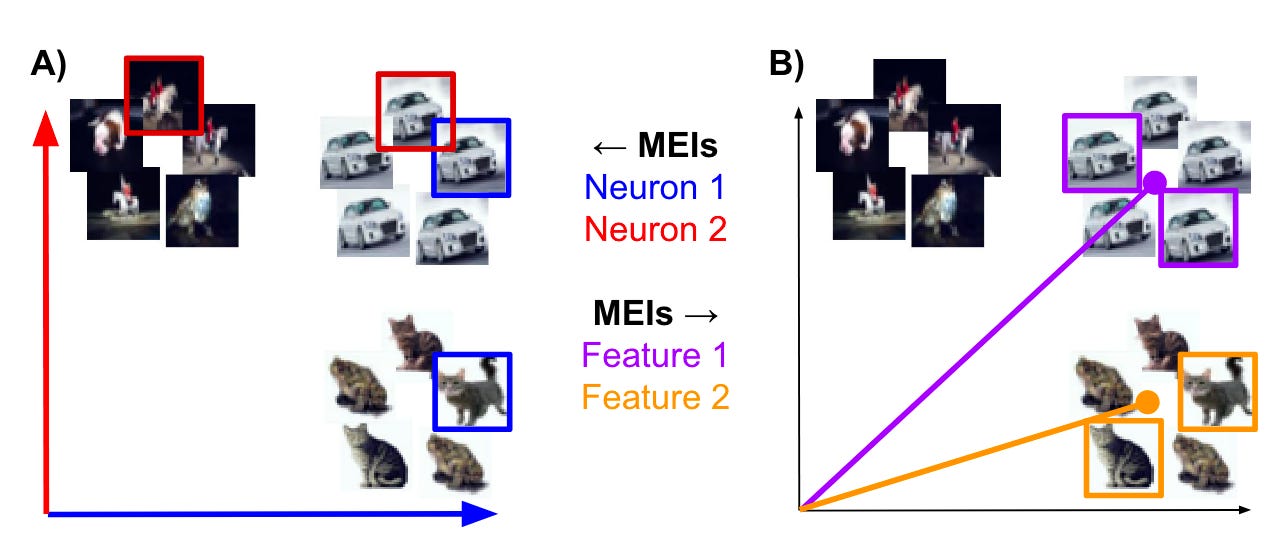
Identifying Interpretable Visual Features in Artificial and Biological Neural Systems | Preprint
Klindt, D., Sanborn, S., Acosta, F., Poitevin, F., Miolane, N.
Many neurons in deep networks exhibit mixed selectivity, representing multiple unrelated features, which supports the hypothesis that features are represented in superposition rather than by individual neurons. We introduce an automated method to quantify visual interpretability and identify meaningful directions in activation space that are more intuitive than single neuron responses. Applying this to both artificial and biological neural data, we find evidence that superposition may underlie robust and efficient representations in the brain as well.
Read More
Geodesic Regression Characterizes 3D Shape Changes in the Female Brain During Menstruation | ICCV-W
Myers, A., Taylor, C., Jacobs, E., Miolane, N.
Women are at increased risk for neurological diseases after menopause, yet the link between brain shape and hormone fluctuations is understudied. We introduce fast approximation methods for geodesic regression on 3D brain surfaces, enabling efficient analysis of shape changes. Applied to real data, our approach reveals how the female hippocampus changes shape across the menstrual cycle in relation to progesterone.
Read More
CryoChains: Heterogeneous Reconstruction of Molecular Assembly of Semi-flexible Chains from Cryo-EM Images | ICML CompBio Workshop
Koo, B., Martel, J., Peck, A., Levy, A., Poitevin, F., Miolane, N.
We propose CryoChains to encode large deformations of biomolecules via rigid body transformation of their polymer instances (chains), while representing their finer shape variations with the normal mode analysis framework of biophysics. CryoChains gives a biophysically-grounded quantification of the heterogeneous conformations of biomolecules, while reconstructing their 3D molecular structures at an improved resolution compared to the current fastest, interpretable deep learning method.
Read More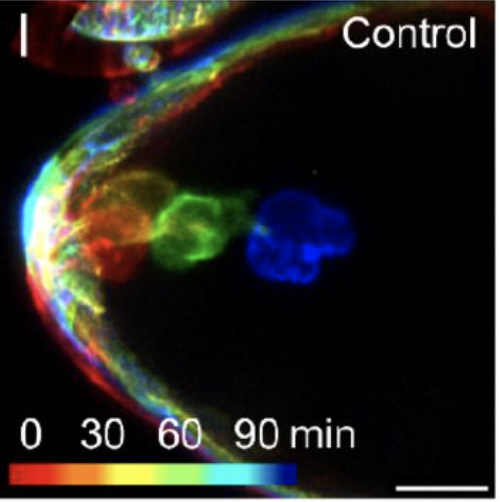
Septins Regulate Border Cell Shape and Surface Geometry ownstream of Rho | Developmental Cell
Gabbert, A., Mondo, J., Campanale, J., Mitchell, N., Myers, A., Streichan, S., Miolane, N., Montell, D.
Septins self-assemble into polymers that bind and deform membranes in vitro and regulate diverse cell behaviors in vivo. How their in vitro properties relate to their in vivo functions is under active investigation. Here we uncover requirements for septins in detachment and motility of border cell clusters in the Drosophila ovary.
Read More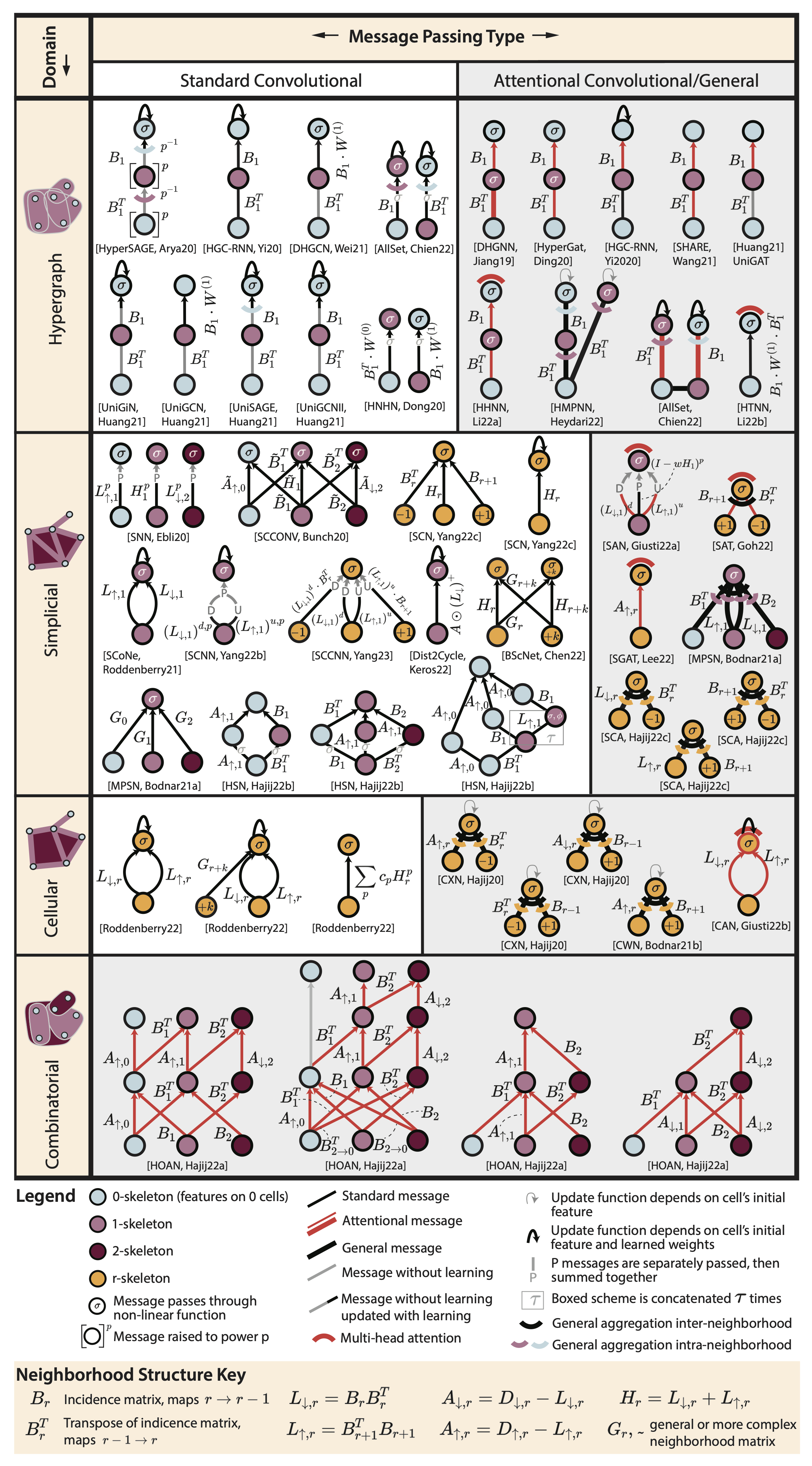
Architectures of Topological Deep Learning: A Survey on Topological Neural Networks | Submitted to tPAMI
Papillon, S., Sanborn, S., Hajij, M., Miolane, N.
Topological Neural Networks (TNNs) extend deep learning to signals on topological domains, enabling the representation of complex systems like proteins and neural activity. This review provides a unified mathematical introduction to TNNs and their latest advancements.
Read More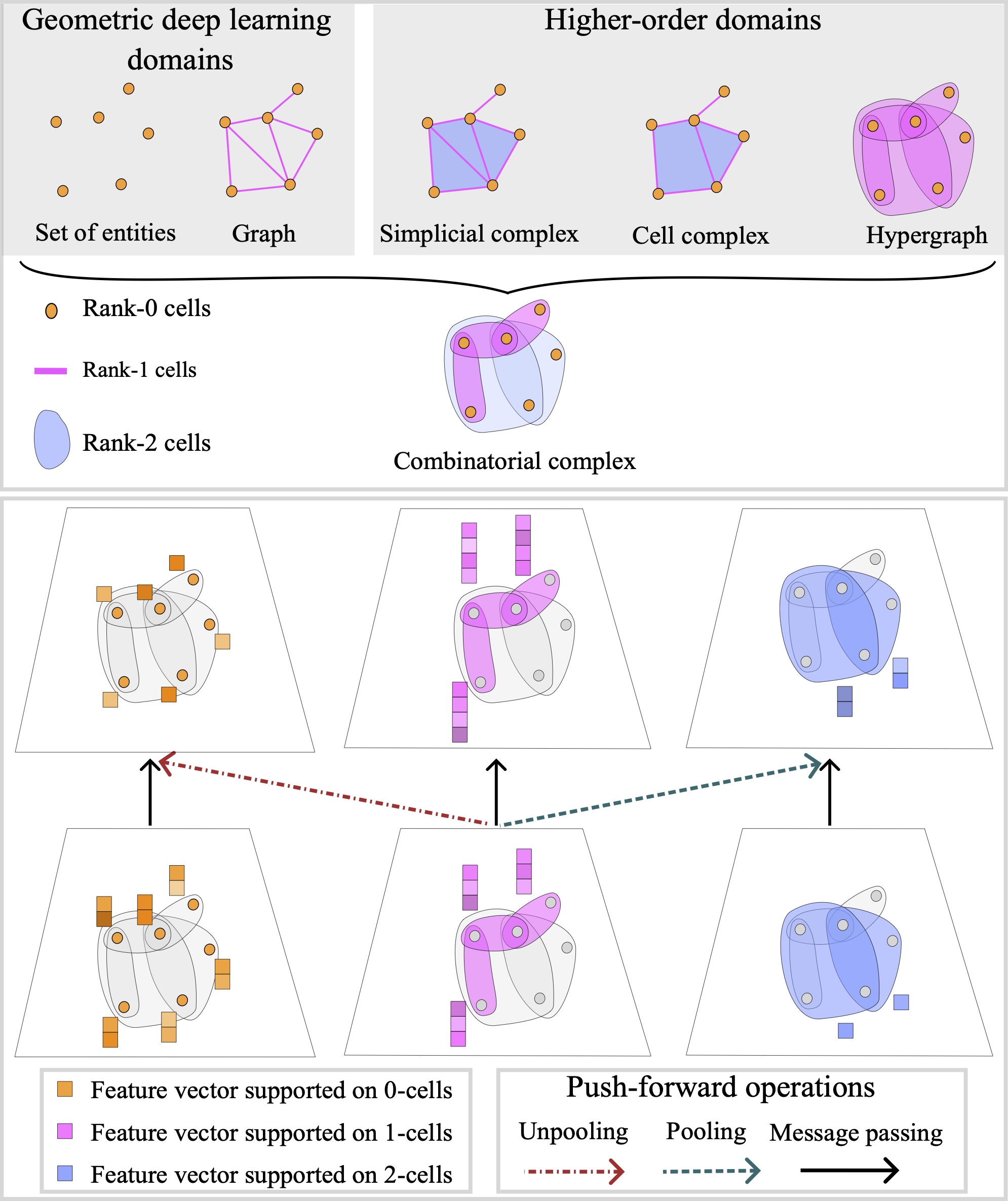
Topological Deep Learning: Going Beyond Graph Data | Textbook
Hajij, M., Zamzmi, G., Papamarkou, T., Miolane, N., Guzmán-Sáenz, A., Ramamurthy, K., Birdal, T., Dey, T., Mukherjee, S., Samaga, S., Livesay, N., Walters, R., Rosen, P., Schaub, M.
Topological deep learning is a rapidly growing field that pertains to the development of deep learning models for data supported on topological domains such as simplicial complexes, cell complexes, and hypergraphs, which generalize many domains encountered in scientific computations. In this paper, we present a unifying deep learning framework built upon a richer data structure that includes widely adopted topological domains.
Read More
Orthogonal Outlier Detection and Dimension Estimation for Improved MDS Embedding of Biological Datasets | Frontiers in Bioinformatics
Li, W., Mirone, J., Prasad, A., Miolane, N., Legrand, C. and Dao Duc, K.
Conventional dimensionality reduction methods are sensitive to orthogonal outliers, which yield significant defects in the embedding. We introduce a robust method to address this problem for cell morphology and human microbiomes datasets.
Read More
Quantifying Extrinsic Curvatures of Neural Manifolds | CVPRW
Acosta, F., Sanborn, S., Dao Duc, K., Madhav, M., Miolane, N.
We leverage tools from Riemannian geometry and topologically-aware deep generative models to introduce a novel approach for studying the geometry of neural manifolds. This approach (1) computes an explicit parameterization of the manifolds and (2) estimates their local extrinsic curvature.
Read More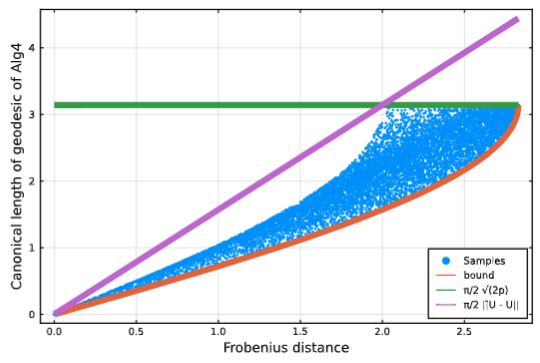
Lipschitz Constants Between Riemannian Metrics on the Stiefel Manifold | Geometric Science of Information
Mataigne, S., Absil, P.-A., Miolane, N.
We give the best Lipschitz constants between the distances induced by any two members of a one-parameter family of Riemannian metrics on the Stiefel manifold of orthonormal p-frames in n dimensions.
Read More
Using an Elastic Metric for Statistical Analysis of Tumor Cell Shape Heterogeneity | Geometric Science of Information
Li, W., Prasad, A., Miolane, N., Dao Duc, K. Geometric Science of Information (GSI): Session Biological Shape Analysis. (Oral)
We propose a methodology grounded in geometric statistics to study and compare cellular morphologies from the contours they form on planar surfaces. We present findings on a dataset of images from osteocarcoma cells that includes different cancer treatments known to affect the cell morphology.
Read More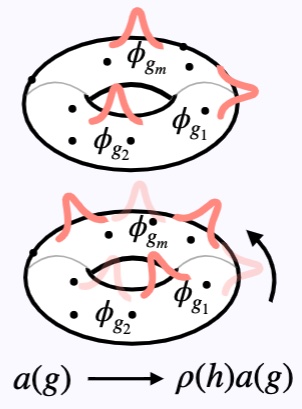
Equivariant Sparse Coding | Geometric Science of Information
Shewmake, C., Miolane, N., Olshausen, B. Geometric Science of Information. (Oral)
We describe a sparse coding model of visual cortex that encodes image transformations in an equivariant manner. We present results on time-varying visual scenes.
Read More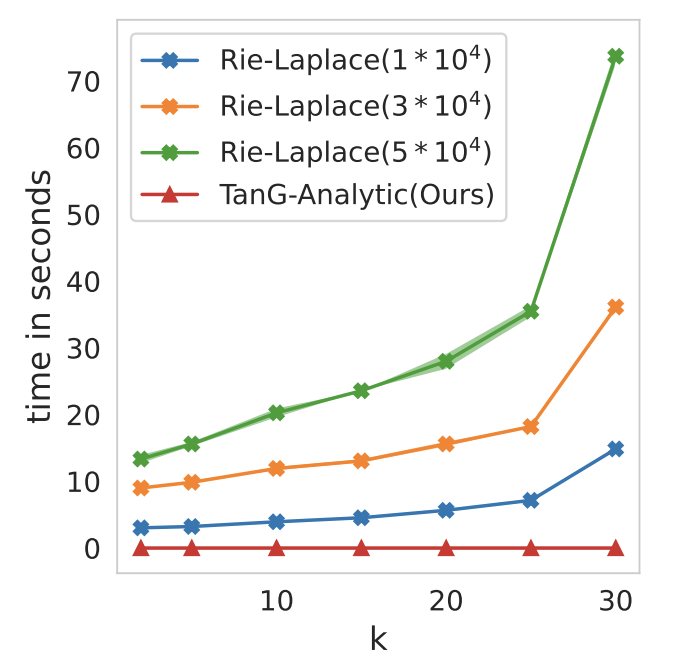
Differentially Private Fréchet Mean on the Manifold of Symmetric Positive Definite (SPD) Matrices | TMLR
Utpala, S., Vepakomma, P., Miolane, N.
Transactions of Machine Learning Research (TMLR).
We introduce the Tangent Gaussian mechanism for computing a differentially private Fréchet mean on the SPD manifold, achieving quadratic utility improvement in data dimension, eliminating the need for Markov Chain Monte Carlo MCMC sampling, and significantly boosting computational efficiency.
Read More
Deep Generative Modeling for Volume Reconstruction in Cryo-Electron Microscopy | JSB
Donnat, C., Levy, A., Poitevin, F., Zhong, E., Miolane, N.
Journal of Structural Biology.
This review examines recent advances in deep generative modeling for cryo-EM reconstruction, highlighting opportunities and challenges in leveraging unsupervised deep learning techniques for high-resolution biomolecular imaging.
Read More
Probabilistic Riemannian Functional Map Synchronization for 3D Shape Correspondence | arXiv
Huq, F., Dey, A., Yusuf, S., Bazazian, D., Birdal, T., Miolane, N.
We address graph-matching on 3D shapes with uncertainty quantification, using functional maps represented on the Lie group SO(n) to model correspondences and synchronization to ensure cycle consistency, improving accuracy across the shape network.
Read More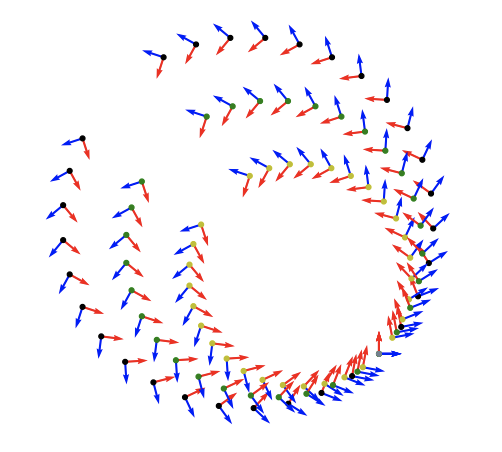
Introduction to Riemannian Geometry and Geometric Statistics: from theory to implementation with Geomstats | JFTML
Guigui, N., Miolane, N., Pennec, X.
Journal of Foundations and Trends in Machine Learning.
This work provides an accessible introduction to Riemannian geometry, including its implementation in Geomstats for statistical and machine learning applications on manifolds, emphasizing computational examples and ease of use akin to scikit-learn.
Read More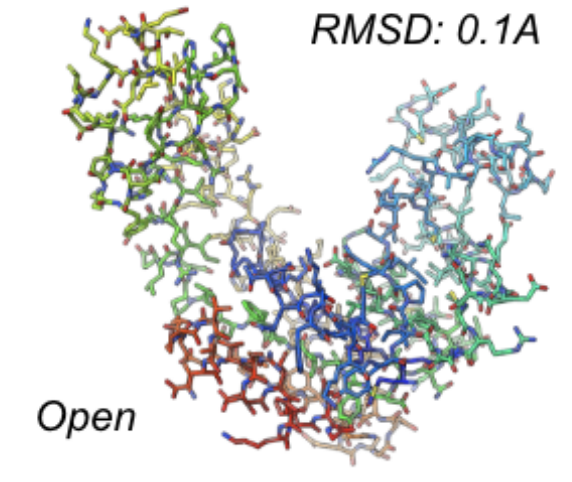
Heterogeneous Reconstructions of Deformable Models in Cryo-Electron Microscopy | NeurIPS MLSB
Nashed, Y., Peck, A., Martel, J., Levy, A., Koo, B., Wetzstein, G., Miolane, N., Ratner, D., Poitevin, F.
NeurIPS Workshop of Machine Learning for Structural Biology.
Cryogenic electron microscopy (cryo-EM) provides a unique opportunity to study the structural heterogeneity of biomolecules. Being able to explain this heterogeneity with atomic models would help our understanding of their functional mechanisms but the size and ruggedness of the structural space (the space of atomic 3D cartesian coordinates) presents an immense challenge. Here, we describe a heterogeneous reconstruction method based on an atomistic representation whose deformation is reduced to a handful of collective motions through normal mode analysis.
Read More
Testing Geometric Representation Hypotheses from Simulated Place Cells Recordings | NeurIPS NeurReps
Niederhauser, T., Lester, A., Miolane, N., Dao Duc, K., Madhav, M.
NeurIPS Workshop for Symmetry and Geometry in Neural Representations.
Hippocampal place cells can encode spatial locations of an animal in physical or task-relevant spaces. We simulated place cell populations that encoded either Euclidean- or graph-based positions of a rat navigating to goal nodes in a maze with a graph topology, and used manifold learning methods to analyze these neural population activities. [Code].
Read More
Regression-Based Elastic Metric Learning on Shape Spaces of Elastic Curves | NeurIPS LMRL
Myers, A., Miolane, N.
NeurIPS Workshop on Learning Meaningful Representations of Life.
We propose a metric learning paradigm, Regression-based Elastic Metric Learning (REML), which optimizes the elastic metric for geodesic regression on the manifold of discrete curves. Geodesic regression is most accurate when the chosen metric models the data trajectory close to a geodesic on the discrete curve manifold. When tested on cell shape trajectories, regression with REML's learned metric has better predictive power than with the conventionally used square-root-velocity (SRV) metric. [Code].
Read More
ICLR 2022 Challenge for Computational Geometry and Topology: Design and Results | PMLR
Myers, A., Utpala, ., Talbar, S., Sanborn, S., Shewmake, C., Donnat, C., Mathe, J., Lupo, U., Sonthalia, R., Cui, X., Szwagier, T., Pignet, A., Bergsson, A., Hauberg, S., Nielsen, D., Sommer, S., Klindt, D., Hermansen, E., Vaupel, M., Dunn, B., Xiong, J., Aharony, N., Pe'er, I., Ambellan, F., Hanik, M., Nava-Yazdani, E., von Tycowicz, C., Miolane, N.
ICLR Geometrical and Topological Representation Learning.
Proceedings of Machine Learning Research.
We present the computational challenge on differential geometry and topology that was hosted within the ICLR 2022 workshop "Geometric and Topological Representation Learning". The competition asked participants to provide implementations of machine learning algorithms on manifolds that would respect the API of the open-source software Geomstats (manifold part) and Scikit-Learn (machine learning part) or PyTorch. [Code].
Read More
Defining an Action of SO(d)-Rotations on Projections of d-Dimensional Objects: Applications to Pose Inference with Geometric VAEs | GRETSI
Legendre, N, Dao Duc, K., Miolane, N.
GRETSI Conference (2022).
Recent advances in variational autoencoders (VAEs) have enabled learning latent manifolds as compact Lie groups, such as SO(d). Since this approach assumes that data lies on a subspace that is homeomorphic to the Lie group itself, we here investigate how this assumption holds in the context of images that are generated by projecting a d-dimensional volume with unknown pose in SO(d).
Read More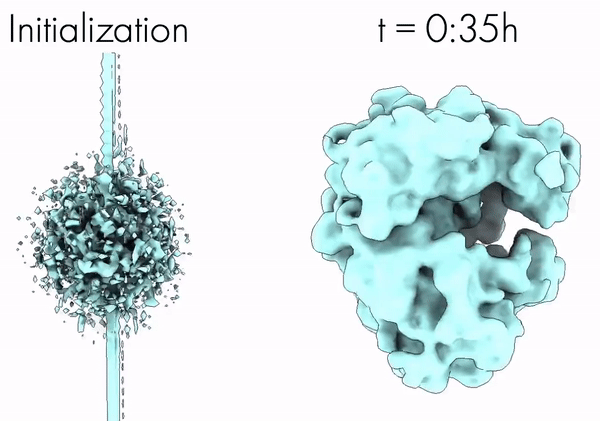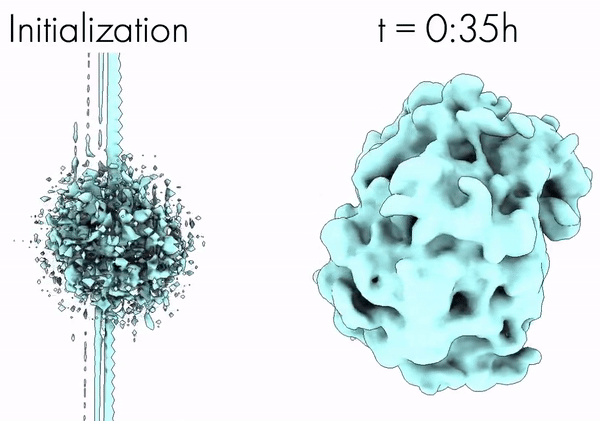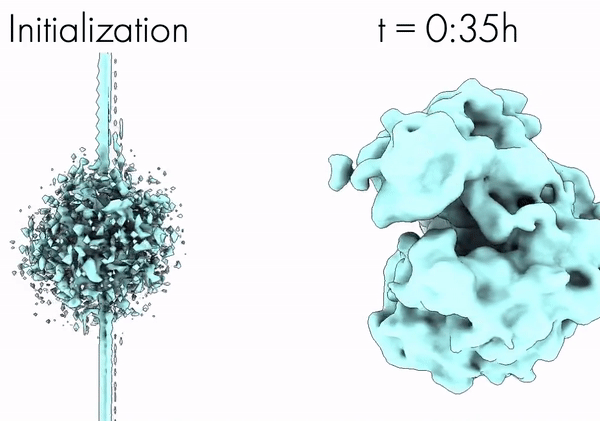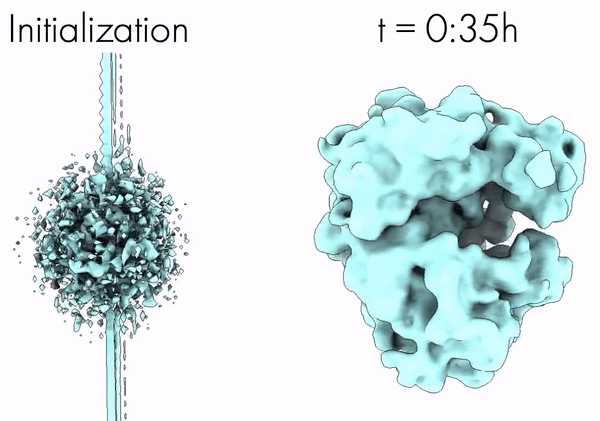
CryoAI: Amortized Inference of Poses for Ab Initio Reconstruction of 3D Molecular Volumes from Real Cryo-EM Images | ECCV
Levy, A., Poitevin, F., Martel, J., Nashed, Y., Peck, A., Miolane, N., Ratner, D., Dunne, M., Wetzstein, G.
4th International Symposium on Cryo-3D Image Analysis (Best Poster Award).
ECCV European Conference on Computer Vision.
Cryo-electron microscopy (cryo-EM) has become a tool of fundamental importance in structural biology. The algorithmic challenge of cryo-EM is to jointly estimate the unknown 3D poses and the 3D electron scattering potential of a biomolecule from millions of extremely noisy 2D images. Existing reconstruction algorithms, however, cannot easily keep pace with the rapidly growing size of cryo-EM datasets due to their high computational and memory cost. We introduce cryoAI, an ab initio reconstruction algorithm for homogeneous conformations that uses direct gradient-based optimization of particle poses and the electron scattering potential from single-particle cryo-EM data. [Code].
Read More
Parametric Information Geometry with the Package Geomstats | Transactions of Mathematical Software (TOMS)
Le Brigant, A., Deschamps, J., Collas, A., Miolane, N.
We introduce the information geometry module of the Python package Geomstats. The module first implements Fisher-Rao Riemannian manifolds of widely used parametric families of probability distributions, such as normal, gamma, beta, Dirichlet distributions, and more. The module further gives the Fisher-Rao Riemannian geometry of any parametric family of distributions of interest, given a parameterized probability density function as input. [Code].
Read More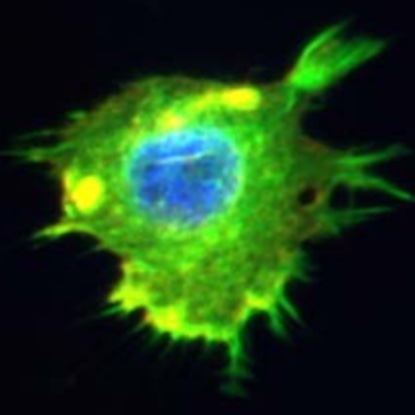
Biological Shape Analysis with Geometric Statistics and Learning | Oberwolfach Snapshots
Utpala, S., Miolane, N.
Oberwolfach Snapshots of Modern Mathematics (2022).
The advances in biomedical imaging techniques have enabled us to access the 3D shapes of a variety of structures: organs, cells, proteins. Since biological shapes are related to physiological functions, shape data may hold the key to unlocking outstanding mysteries in biomedicine. This snapshot introduces the mathematical framework of geometric statistics and learning and its applications in biomedicine.
Read More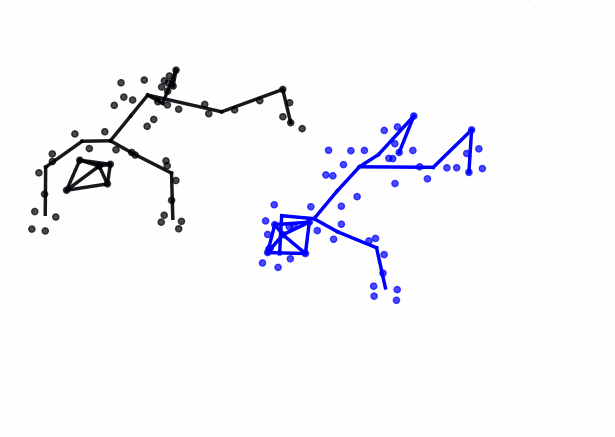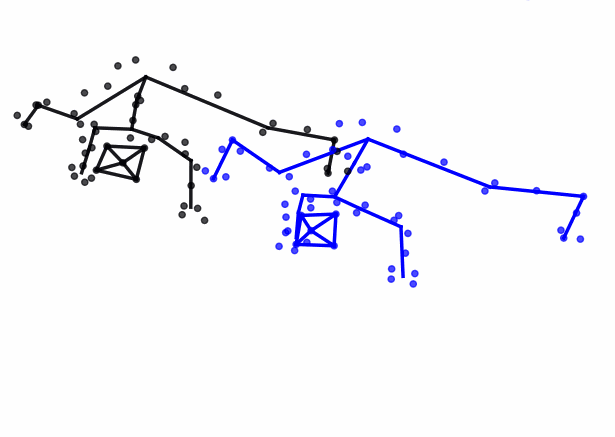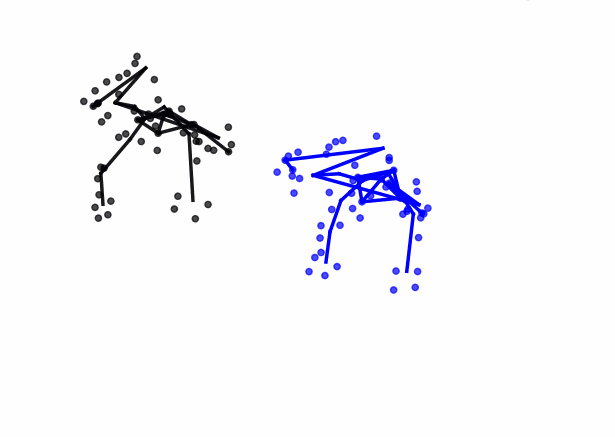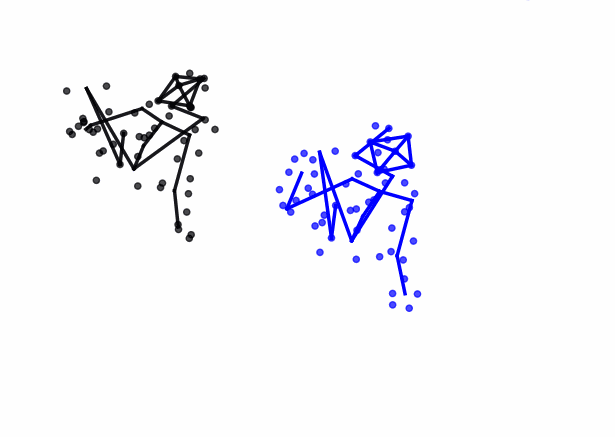
Intentional Choreography with Semi-Supervised Recurrent Variational Autoencoders | NeurIPS CAD
Papillon, M., Pettee, M., Miolane, N.
NeurIPS Workshop of Creativity and Design.
Given a small amount of dance sequences labeled with qualitative choreographic annotations, PirouNet conditionally generates dance sequences in the artistic style of the choreographer. [Code].
Read More
PirouNet: Creating Dance through Artist-Centric Deep Learning | EAI ArtsIT
Papillon M., Pettee M., Miolane N.
EAI ArtsIT Conference. Best Paper Award (Oral).
Using Artificial Intelligence (AI) to create dance choreography with intention is still at an early stage. Methods that conditionally generate dance sequences remain limited in their ability to follow choreographer-specific creative direction, often relying on external prompts or supervised learning. In the same vein, fully annotated dance datasets are rare and labor intensive. To fill this gap and help leverage deep learning as a meaningful tool for choreographers, we propose "PirouNet": PirouNet allows dance professionals to annotate data with their own subjective creative labels and subsequently generate new bouts of choreography based on their aesthetic criteria. Thanks to the proposed semi-supervised approach, PirouNet only requires a small portion of the dataset to be labeled, typically on the order of 1%.. [Code].
Read More
Higher-Order Attention Networks | ArXiv
Hajij, M., Zamzmi, G., Papamarkou, T., Miolane, N., Guzman-Saenz, A., Ramamurthy, K., N.
We introduce higher-order attention networks (HOANs), a novel class of attention-based neural networks defined on a generalized higher-order domain called a combinatorial complex (CC). Similar to hypergraphs, CCs admit arbitrary set-like relations between a collection of abstract entities. Simultaneously, CCs permit the construction of hierarchical higher-order relations analogous to those supported by cell complexes. Thus, CCs effectively generalize both hypergraphs and cell complexes and combine their desirable characteristics.
Read More
ICLR 2021 Challenge for Computational Geometry and Topology: Design and Results | PMLR
Miolane, N., Caorsi, M., Lupo, U., Guerard, M., Guigui, N., Mathe, J., Cabanes, Y., Reise, W., Davies, T., Leitão, A., Mohapatra, S., Utpala, S., Shailja, S., Corso, G., Liu, G., Iuricich, F., Manolache, A., Nistor, M., Bejan, M., Mihai Nicolicioiu, A., Luchian, B.-A., Stupariu, M.-S., Michel, F., Dao Duc, K., Abdulrahman, B., Beketov, M., Maignant, E., Liu, Z., Černý, M., Bauw, M., Velasco-Forero, S., Angulo, J., Long Y.
ICLR Workshop on Geometrical and Topologic Representation Learning.
Proceedings of Machine Learning Research (PMLR).
We present the computational challenge on differential geometry and topology that happened within the ICLR 2021 workshop "Geometric and Topological Representation Learning". The competition asked participants to provide creative contributions to the fields of computational geometry and topology through the open-source repositories Geomstats and Giotto-TDA. [Code].
Read More
Geomstats: A Python Package for Riemannian Geometry in Machine Learning | JMLR
Miolane, N., Guigui, N., Le Brigant, A., Mathe, J., Hou, B., Thanwerdas, Y., Heyder, S., Peltre, O., Koep, N., Cabanes, Y., Chauchat, P., Zaatiti, H., Hajri, H., Gerald, T. , Shewmake, C., Brooks, D., Kainz, B., Donnat, C., Holmes, S., Pennec, X.
Journal of Machine Learning Research.
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. [Code].
Read More
Introduction to Geometric Learning in Python with Geomstats | SciPy
Miolane, N., Guigui, N., Zaatiti, H., Shewmake, C., Hajri, H., Brooks, D., Le Brigant, A., Mathe, J. Hou, B., Thanwerdas, Y., Heyder, S., Peltre, O., Koep, N., Cabanes, Y., Gerald, T. Chauchat, P., Kainz, B., Donnat, C., Holmes, S., Pennec, X.
SciPy Conference on Scientific Computing in Python.
There is a growing interest in leveraging differential geometry in the machine learning community. Yet, the adoption of the associated geometric computations has been inhibited by the lack of a reference implementation. To address this gap, we present the open-source Python package geomstats and introduce hands-on tutorials for differential geometry and geometric machine learning algorithms. [Code].
Read More
Learning Weighted Submanifolds With Riemannian Variational Autoencoders | CVPR
Miolane, N., Holmes, S.
CVPR Conference of Computer Vision and Pattern Recognition.
Manifold-valued data naturally arises in medical imaging. One of the challenges that naturally arises consists of finding a lower-dimensional subspace for representing such manifold-valued data. Traditional techniques, like principal component analysis, are ill-adapted to tackle non-Euclidean spaces. We introduce Riemannian Variational Autoencoders to perform weighted submanifold learning powered by amortized variational inference.
Read More
Estimation of Orientation and Camera Parameters from Cryo-Electron Microscopy Images with Variational Autoencoders and Generative Adversarial Networks | CVPRW
Miolane, N., Poitevin, F., Li, Y.-T., Holmes, S.
CVPR Workshop on Computer Vision for Microscopy Imaging.
We combine variational autoencoders (VAEs) and generative adversarial networks (GANs) to learn a low-dimensional latent representation of cryo-EM images. Cryo-electron microscopy (cryo-EM) is capable of producing reconstructed 3D images of biomolecules at near-atomic resolution. As such, it represents one of the most promising imaging techniques in structural biology.
Read More
A Bayesian Hierarchical Network for Combining Heterogeneous Data Sources in Medical Diagnoses | NeurIPS ML4H
Donnat, C., Miolane, N., Bunbury, F., Kreindler, J.
NeurIPS Workshop on Machine Learning for Health.
1st Prize: C3.ai Grand Covid Challenge (100,000$).
Computer-Aided Diagnosis has shown stellar performance in providing accurate medical diagnoses across multiple testing modalities (medical images, electrophysiological signals, etc.). While this field has typically focused on fully harvesting the signal provided by a single (and generally extremely reliable) modality, fewer efforts have utilized imprecise data lacking reliable ground truth labels. We devise a Stochastic Expectation-Maximization algorithm that allows the principled integration of heterogeneous, and potentially unreliable, data types. We showcase the practicality of this approach by deploying it on a real COVID-19 immunity study.
Read More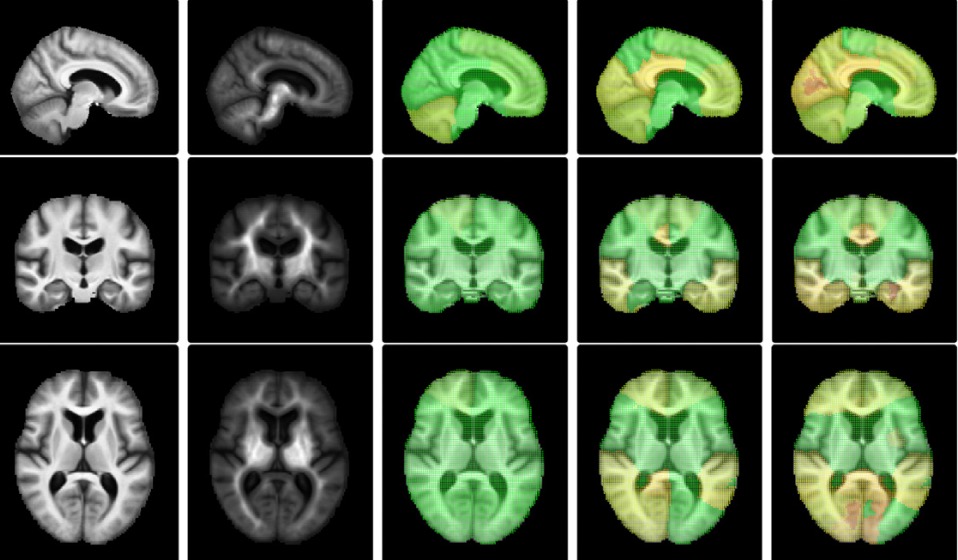
Bias on Estimation in Quotient Space and Correction Methods | Elsevier
Miolane, N., Devilliers, L., Pennec, X.
Chapter in Riemannian Geometric Statistics in Medical Imaging. Statistics on Shape Spaces. Elsevier.
Read More
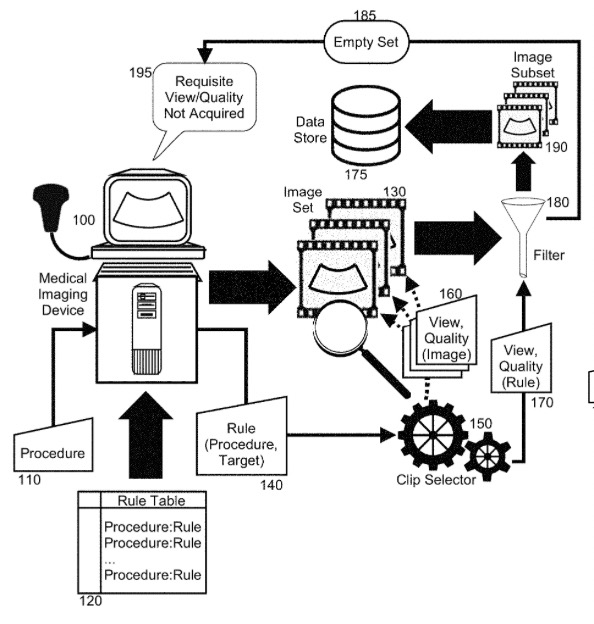
Video Clip Selector for Medical Imaging and Diagnosis | Patent
Koepsell, K., Cadieu, D., Poilvert, N., Hong, H., Cannon, M., Bilenko, N., Romano, N., Mathe, J., Cheng, C., Miolane, N.
Caption Health.
United States Patent and Trademark Office.
Read More
PVNet: A LRCN Architecture for Spatio-Temporal Photovoltaic Power Forecasting from Numerical Weather Prediction | ICML AICC
Mathe, J., Miolane, N., Sebastien, N., Lequeux, J.
ICML Workshop on AI for Climate Change.
Photovoltaic (PV) power generation has emerged as one of the lead renewable energy sources. Yet, its production is characterized by high uncertainty, being dependent on weather conditions like solar irradiance and temperature. Predicting PV production, even in the 24-hour forecast, remains a challenge and leads energy providers to left idling - often carbon emitting - plants. In this paper, we introduce a Long-Term Recurrent Convolutional Network using Numerical Weather Predictions (NWP) to predict, in turn, PV production in the 24-hour and 48-hour forecast horizons. This network architecture fully leverages both temporal and spatial weather data, sampled over the whole geographical area of interest. We train our model on an NWP dataset from the National Oceanic and Atmospheric Administration (NOAA) to predict spatially aggregated PV production in Germany. We compare its performance to the persistence model and state-of-the-art methods.
Read More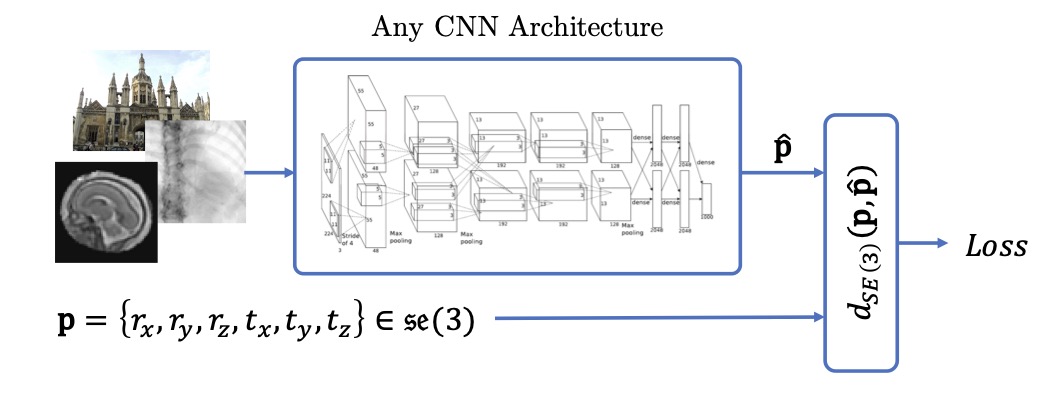
Computing CNN Loss and Gradients for Pose Estimation with Riemannian Geometry | MICCAI
Hou, B., Miolane N., Khanal B., Lee M., Alansary A., McDonagh S., Hajnal J., Rueckert D., Glocker B., Kainz B.
MICCAI Conference on Medical Image Computing and Computer Assisted Intervention.
Pose estimation, i.e. predicting a 3D rigid transformation with respect to a fixed co-ordinate frame in, SE(3), is an omnipresent problem in medical image analysis with applications such as: image rigid registration, anatomical standard plane detection, tracking and device/camera pose estimation. Deep learning methods often parameterise a pose with a representation that separates rotation and translation. As commonly available frameworks do not provide means to calculate loss on a manifold, regression is usually performed using the L2-norm independently on the rotation's and the translation's parameterisations, which is a metric for linear spaces that does not take into account the Lie group structure of SE(3). In this paper, we propose a general Riemannian formulation of the pose estimation problem. We propose to train the CNN directly on SE(3) equipped with a left-invariant Riemannian metric, coupling the prediction of the translation and rotation defining the pose. At each training step, the ground truth and predicted pose are elements of the manifold, where the loss is calculated as the Riemannian geodesic distance. We then compute the optimisation direction by back-propagating the gradient with respect to the predicted pose on the tangent space of the manifold SE(3) and update the network weights. We thoroughly evaluate the effectiveness of our loss function by comparing its performance with popular and most commonly used existing methods, on tasks such as image-based localisation and intensity-based 2D/3D registration. We also show that hyper-parameters, used in our loss function to weight the contribution between rotations and translations, can be intrinsically calculated from the dataset to achieve greater performance margins.
Read More
Topologically Constrained Template Estimation | SIAGA
Miolane, N., Holmes, S., Pennec, X.
SIAM Journal on Applied Algebra and Geometry.
In most neuroimaging studies, one builds a brain template that serves as a reference for normalizing the measurements of each individual subject into a common space. Such a template should be representative of the population under study, thus avoiding bias in subsequent statistical analyses. The template is often computed by iteratively registering all images to the current template and then averaging the intensities of the registered images. Geometrically, the procedure can be summarized as the computation of the template as the “Fréchet mean” of the images projected in a quotient space. It has been argued recently that this type of algorithm could actually be asymptotically biased and therefore inconsistent. In other words, even with an infinite number of brain images in the database, the template estimate may not converge to the brain anatomy it is meant to estimate. Our paper investigates this phenomenon. We present a methodology that spatially quantifies the brain template's asymptotic bias. We identify the main variables that influence inconsistency. This leads us to investigate the topology of the template's intensity level sets, represented by its Morse--Smale (MS) complex. We propose a topologically constrained adaptation of the template computation that constructs a hierarchical template with bounded bias. We apply our method to the analysis of a brain template of 136 T1 weighted MR images from the Open Access Series of Imaging Studies (OASIS) database.
Read More
Template Shape Estimation in Computational Anatomy | SIIMS
Miolane, N., Holmes, S., Pennec, X.
SIAM Journal of Imaging Science.
We use tools from geometric statistics to analyze the usual estimation procedure of a template shape. This applies to shapes from landmarks, curves, surfaces, images etc. We demonstrate the asymptotic bias of the template shape estimation using the stratified geometry of the shape space. We give a Taylor expansion of the bias with respect to a parameter σ describing the measurement error on the data. We propose two bootstrap procedures that quantify the bias and correct it, if needed. They are applicable for any type of shape data. We give a rule of thumb to provide intuition on whether the bias has to be corrected. This exhibits the parameters that control the bias’ magnitude. We illustrate our results on simulated and real shape data.
Read More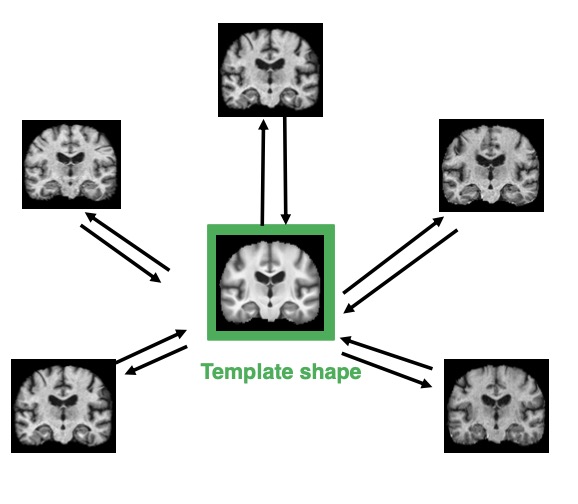
Toward a Unified Geometric Bayesian Framework for Template Estimation in Computational Anatomy. | ISBA
Miolane, N., Pennec, X., Holmes, S.
ISBA World Meeting of the International Society for Bayesian Analysis. (Young Researcher Travel Award).
Computational Anatomy aims to model and analyze the variability of the human anatomy. Given a set of medical images of the same organ, the first step is the estimation of the mean organ’s shape. This mean anatomical shape is called the template in Computer vision or Medical imaging. The estimation of a template/atlas is central because it represents the starting point for all further processing or analyses. In view of the medical applications, evaluating the quality of this statistical estimate is crucial. How does the estimated template behave for varying amount of data, for small and large level of noise? We present a geometric Bayesian framework which unifies two estimation problems that are usually considered distinct: the template estimation problem and manifold learning problem - here associated to estimating the template’s orbit. We leverage this to evaluate the quality of the template estimator.
Read More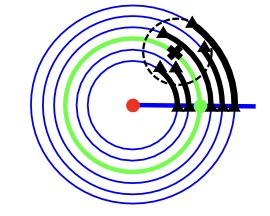
Biased Estimators on Quotient spaces | GSI
Miolane, N., Pennec, X.
Conference on Geometric Sciences of Information. (Oral). [Video].
Usual statistics are defined, studied and implemented on Euclidean spaces. But what about statistics on other mathematical spaces, like manifolds with additional properties: Lie groups, Quotient spaces, Stratified spaces etc. How can we describe the interaction between statistics and geometry? The structure of Quotient space in particular is widely used to model data, for example every time one deals with shape data. These can be shapes of constellations in Astronomy, shapes of human organs in Computational Anatomy, shapes of skulls in Palaeontology, etc. Given this broad field of applications, statistics on shapes -and more generally on observations belonging to quotient spaces- have been studied since the 1980's. However, most theories model the variability in the shapes but do not take into account the noise on the observations themselves. In this paper, we show that statistics on quotient spaces are biased and even inconsistent when one takes into account the noise. In particular, some algorithms of template estimation in Computational Anatomy are biased and inconsistent. Our development thus gives a first theoretical geometric explanation of an experimentally observed phenomenon. A biased estimator is not necessarily a problem. In statistics, it is a general rule of thumb that a bias can be neglected for example when it represents less than 0.25 of the variance of the estimator. We can also think about neglecting the bias when it is low compared to the signal we estimate. In view of the applications, we thus characterize geometrically the situations when the bias can be neglected with respect to the situations when it must be corrected.
Read More
Mathematical Structures for Extending 2D Neurogeometry to 3D Image Processing | MICCAI MCV
Miolane, N., Pennec, X.
MICCAI Workshop of Medical Computer Vision. [Code].
In the era of big data, one may apply generic learning algorithms for medical computer vision. But such algorithms are often "black-boxes" and as such, hard to interpret. We still need new constructive models, which could eventually feed the big data framework. Where can one find inspiration for new models in medical computer vision? The emerging field of Neurogeometry provides innovative ideas. Neurogeometry models the visual cortex through modern Differential Geometry: the neuronal architecture is represented as a sub-Riemannian manifold R2 x S1. On the one hand, Neurogeometry explains visual phenomena like human perceptual completion. On the other hand, it provides efficient algorithms for computer vision. Examples of applications are image completion (in-painting) and crossing-preserving smoothing. In medical image computer vision, Neurogeometry is less known although some algorithms exist. One reason is that one often deals with 3D images, whereas Neurogeometry is essentially 2D (our retina is 2D). Moreover, the generalization of (2D)-Neurogeometry to 3D is not straight-forward from the mathematical point of view. This article presents the theoretical framework of a 3D-Neurogeometry inspired by the 2D case. We survey the mathematical structures and a standard frame for algorithms in 3D- Neurogeometry. The aim of the paper is to provide a "theoretical toolbox" and inspiration for new algorithms in 3D medical computer vision.
Read More

Computing Bi-Invariant Pseudo-Metrics on Lie Groups | Entropy
Miolane, N., Pennec, X.
Journal Entropy. [Code].
In computational anatomy, organ’s shapes are often modeled as deformations of a reference shape, i.e., as elements of a Lie group. To analyze the variability of the human anatomy in this framework, we need to perform statistics on Lie groups. A Lie group is a manifold with a consistent group structure. Statistics on Riemannian manifolds have been well studied, but to use the statistical Riemannian framework on Lie groups, one needs to define a Riemannian metric compatible with the group structure: a bi-invariant metric. However, it is known that Lie groups, which are not a direct product of compact and abelian groups, have no bi-invariant metric. However, what about bi-invariant pseudo-metrics? In other words: could we remove the assumption of the positivity of the metric and obtain consistent statistics on Lie groups through the pseudo-Riemannian framework? Our contribution is two-fold. First, we present an algorithm that constructs bi-invariant pseudo-metrics on a given Lie group, in the case of existence. Then, by running the algorithm on commonly-used Lie groups, we show that most of them do not admit any bi-invariant (pseudo-) metric. We thus conclude that the (pseudo-) Riemannian setting is too limited for the definition of consistent statistics on general Lie groups.
Read More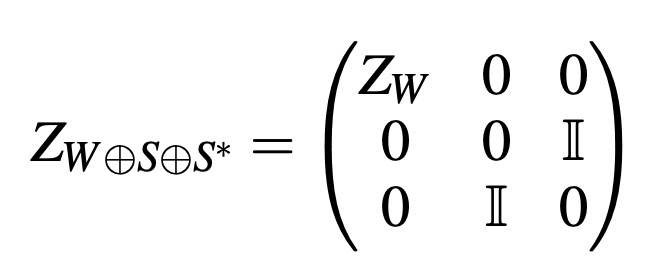
Statistics on Lie Groups | MaxEnt
Miolane, N., Pennec, X.
MaxEnt Workshop on Bayesian Inference and Maximum Entropy Methods. (Oral). [Code].
Lie groups appear in many fields from Medical Imaging to Robotics. In Medical Imaging and particularly in Computational Anatomy, an organ’s shape is often modeled as the deformation of a reference shape, in other words: as an element of a Lie group. In this framework, if one wants to model the variability of the human anatomy, e.g. in order to help diagnosis of diseases, one needs to perform statistics on Lie groups. A Lie group 𝒢 is a manifold that carries an additional group structure. Statistics on Riemannian manifolds have been well studied with the pioneer work of Fréchet, Karcher and Kendall [1, 2, 3, 4] followed by others [5, 6, 7, 8, 9]. In order to use such a Riemannian structure for statistics on Lie groups, one needs to define a Riemannian metric that is compatible with the group structure, i.e a bi-invariant metric. However, it is well known that general Lie groups which cannot be decomposed into the direct product of compact and abelian groups do not admit a bi-invariant metric. One may wonder if removing the positivity of the metric, thus asking only for a bi-invariant pseudo-Riemannian metric, would be sufficient for most of the groups used in Computational Anatomy. In this paper, we provide an algorithmic procedure that constructs bi-invariant pseudo-metrics on a given Lie group 𝒢. The procedure relies on a classification theorem of Medina and Revoy. However in doing so, we prove that most Lie groups do not admit any bi-invariant (pseudo-) metric. We conclude that the (pseudo-) Riemannian setting is not the richest setting if one wants to perform statistics on Lie groups. One may have to rely on another framework, such as affine connection space.
Read MoreAnalyse Biométrique de l'Anneau Pelvien en 3 Dimensions | JRCOT
Darmante, H., Bugnas, B., Dompsure, R.B.D., Barresi, L., Miolane, N., Pennec, X., de Peretti, F., Bronsard, N.
Journal Revue de Chirurgie Orthopédique et Traumatologique.
Read More
Defining a Mean on Lie Groups | Imperial College London
Miolane, N.
Statistics are mostly performed in vector spaces, flat structures where the computations are linear. When one wants to generalize this setting to the non-linear structure of Lie groups, it is necessary to redefine the core concepts. For instance, the linear definition of the mean as an integral can not be used anymore. In this thesis, we investigate three possible definitions depending of the Lie group geometric structure. First, we import on Lie groups the notion of Riemannian center of mass (CoM) which is used to define a mean on manifolds and investigate when it can define a mean which is compatible with the algebraic structure. It is the case only for a small class of Lie groups. Thus we extend the CoM’s definition with two others: the Riemannian exponential barycenter and the group exponential barycenter. This thesis investigates how they can define admissible means on Lie groups.
Read More
